Two twists on a graph

So, something that shouldn't be terribly surprising is that one can take a graph (edges and vertices) and represent it as a set of vertices. This innocent-looking cube will be our example:

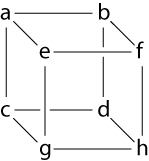
edge(a, b)    edge(a, c) edge(c, d) edge(b, d) edge(a, e) edge(b, f)

edge(c, g)    edge(d, h) edge(e, f) edge(e, g) edge(g, h) edge(f, h)

vertex(a) vertex(b) vertex(c) vertex(d) vertex(e) vertex(f) vertex(g) vertex(h)

We'll collect this set of facts and call the collection of propositions (20 atomic propositions in all) GRAPH.

Also not terribly interesting, but maybe ever-so-slightly interesting, is that one can take this representation of a graph and do forward-chaining logic programming with it. Consider, for example, the following forward-chaining logic program made up of two rules.

  edge(Y,X) <- edge(X,Y).
  reachable(Y) <- edge(X,Y), reachable(X), vertex(Y).

These are just logical propositions; the upper-case identifiers are implicitly universally quantified, the comma represents conjunction, and (following common convention for logic programming) we write implication backwards as B <- A instead of A -> B. We'll call this collection of two rules REACH.

Recall that the behavior of a forward chaining logic program is to take facts that it has and learn more facts. If we just throw the graph at this program, it will use the first rule to derive all the backwards edges (edge(b,a), edge(c,a), and so on) but nothing else. If we add an additional single fact reachable(a), then our forward chaining logic program will furiously learn that b, c, and indeed all the other vertices are reachable. We can rephrase this in the following way: for a specific choice of X and Y, there is a path from X to Y if and only if there is a derivation of this sequent:

  GRAPH, REACH ⊢ reachable(X) -> reachable(Y)

In fact, the forward chaining logic programming engine, given reachable(X) for some specific X, will derive a fact of the form reachable(Y) for every reachable Y.

Twist 1: weighted logic programming

The first interesting twist on our boring program is this: we consider those proofs of the sequent

  GRAPH, REACH ⊢ reachable(X) -> reachable(Y)

and we ask, what if some proofs are better than others? One way to introduce a metric for "what is better" is to say that every one of those atomic propositions has a cost, and every time we use that atomic proposition in a proof we have to pay that cost: we want the cheapest proof:

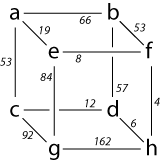edge(a, b) = 66    edge(a, c) = 53 edge(c, d) = 12 edge(b, d) = 57 edge(a, e) = 19 edge(b, f) = 53

edge(c, g) = 92    edge(d, h) = 6 edge(e, f) = 8 edge(e, g) = 84 edge(g, h) = 162 edge(f, h) = 4

vertex(a) = 0 vertex(b) = 0 vertex(c) = 0 vertex(d) = 0 vertex(e) = 0 vertex(f) = 0 vertex(g) = 0 vertex(h) = 0

This sort of problem is amenable to what is called weighted logic programming, a declarative way of specifying dynamic programming problems. In this case, if the edge weights are all positive, this is a declarative way of specifying Dijkstra's algorithm for single-source shortest path. Before, our forward-chaining logic programming engine took a single fact reachable(X) and computed all the nodes reachable from X. Now, our weighted logic programming engine takes a single fact reachable(X) with cost 0 and computes the minimum-cost route to every node reachable from X.

Related work

In fact we can play the same game on any semiring as long as the "score" of a proof is the semiring product of the score of the axioms (in this case, "plus" was the semiring product) and the way we combine the scores of different proofs is the semiring sum of the scores of the two proofs (in this case, "min" was the semiring sum). This sort of generalization-to-an-arbitrary semiring is something that isn't noticed as much as it probably should be. If you're interested in learning or thinking more about weighted logic programming, the first eleven pages of the paper I coauthored with Shay Cohen and Noah Smith, Products of Weighted Logic Programs, were written specifically as a general audience/programming languages audience introduction to weighted logic programming. Most of the other literature on weighted logic programming is by Jason Eisner, though the semiring generalization trick was first extensively covered by Goodman in the paper Semiring Parsing; that paper was part of what inspired Eisner's work on weighted logic programming, at least as I understand it.

Twist 2: linear logic programming

Another direction that we can "twist" this initially graph discussion is by adding linearity. Linear facts (in the sense of linear logic) are unlike "regular" facts - regular facts can be used any number of times or used not at all - they are persistent. Linear facts can only be used once in a proof - and in fact, they must be used once in a proof.

We've had the vertex propositions hanging around all this time and not doing much; one thing we can do is make these vertex propositions linear, and we'll make the reachable propositions linear as well. In this example, we'll designate linear propositions by underlining them and coloring them red; our program before turns into this:

  edge(Y,X) <- edge(X,Y).
  reachable(Y) <- edge(X,Y), reachable(X), vertex(Y).

By the way, if you're familiar with linear logic, the logical meaning of this formula is captured by the following two propositions written properly in linear logic:

  ∀x. ∀y. !edge(x,y) -o edge(y,x).
  ∀x. ∀y. !edge(x,y) -o reachable(x) -o vertex(y) -o reachable(y).

We'll talk a little bit more about this specification (call it LREACH) shortly; for the moment let's switch to a different train of thought.

Greedy logic programming with linear logic

When we talked before about the cost of using a fact in a proof, we were actually assuming a little bit about proofs being focused; we'll talk a little bit about focusing and synthetic rules in this section (see this old blog post for background).

If we make all of our atomic propositions positive, then the synthetic rule associated with the critical second rule above ends up looking like this:

  Γ, edge(X,Y); Δ, reachable(Y) ⊢ C
  ---------------------------------------------
  Γ, edge(X,Y); Δ, reachable(X), vertex(Y) ⊢ C

Recall that we like to read forward chaining rules from the bottom to the top. If we assume that the context only ever contains a single reachable(X) proposition, then we can think of the linear context as a resource consuming automaton that is in state X. At each step, the automaton consumes an available resource vertex(Y) with the constraint that there must be an edge from X to Y; the automaton then transitions to state Y.

One efficient way to give a logic programming semantics to these kind of forward-chaining linear logical specifications is to just implement an arbitrary run of the automaton without ever backtracking. This is a greedy strategy, and it can be used to efficiently implement some greedy algorithms. This was the point of Linear Logical Algorithms, a paper I coauthored with Frank Pfenning. One neat example from that paper was the following graph program, which computes a spanning tree for a graph rooted at the vertex a:

  edge(Y,X) <- edge(X,Y).
  intree(a) <- vertex(a).
  tree(X,Y), intree(Y) <- edge(X, Y), intree(X), vertex(Y).

This program works like another little resource-consuming automaton that, at each step, consumes a vertex resource to add a non-tree vertex to the tree along a newly added tree edge. This is, incidentally, the same way Prim's algorithm for minimum spanning trees progresses.

Hamiltonian paths in linear logic

The greedy strategy where we look at one possible set of choices is very different than the behavior of our briefly-sketched forward-chaining persistent and weighted logic programming engines. The latter worked by taking some initial information (reachable(X) for some X) and finding, all at once and with reasonable efficiency, every single Y for a given X such that the following sequent holds:

  GRAPH, REACH ⊢ reachable(X) -> reachable(Y)

Call the (persistent) edges EDGE, and the (linear) vertices VERT. Now we can look at the (seemingly) analogous problem stated in linear logic to see why it is in practice, so different:

  LREACH, EDGE; VERT ⊢ ⊢ reachable(X) -o reachable(Y)

Because linear logic requires that we eventually use every resource in VERT, this derivation corresponds to a run of the automaton where the automaton visited every single node and then ended at Y. If we consider just the case where X and Y are the same, complete derivations correspond to Hamiltonian tours.

By adding linearity, we've made the forward chaining language more expressive, but in doing so we created a big gulf between the "existential" behavior (here's one way the automaton might work, which we found by being greedy) and the "universal" behavior (the automaton can, potentially, follow a Hamiltonian path, which we learned by calling a SAT solver). This gap did not exist, at least for our running example, in the persistent or weighted cases.

Combining the twists?

Both linear logic programming and weighted logic programming arise start from a simple observation: the shape of proofs can capture interesting structures. The "structure" in this case was a path through a graph; in weighted logic programming the structures are often parse trees - you know, "boy" is a noun, "fast" is an adverb, "the" is a demonstrative adjective, and the two combined are a noun phrase, until you get a tree that looks something like this:

    Sentence 
      /  \
     NP  VP
    /|   | \
  /  |   |  \
 D   N   V   A
 |   |   |   |
the boy ran fast

(More on this in the "Products of Weighted Logic Programs" paper.)

Weighted logic programming enriches this observation by allowing us to measure structures and talk about the combined measure of a whole class of structures; linear logic, on the other hand, greatly improves on the things that we can measure. But what about using the observations of weighted logic programming to assign scores in the richer language of linear logic programming? What would that look like? I'll give a couple of sketches. These are questions I don't know the answers to, don't know that I'll have time to think about in the near future, but would love to talk further about with anybody who was interested.

Minimum spanning tree

I commented before that the logic programming engine described in Linear Logical Algorithms implements something a bit like Prim's algorithm to produce a graph spanning tree. In fact, the engine we described does so with provably optimal complexity - O(|E| + |V|), time proportional to the number of edges in the graph or the number of vertices in the graph (whichever is larger). What's more, we have a good cost semantics for this class of weighted logic programs; this means you don't actually have to understand how the interpreter works, you can reason about the runtime behavior of linear logical algorithms on a much more abstract level. The recorded presentation on Linear Logical Algorithms, as well as the paper, discuss this.

If we replace a queue inside the engine with an appropriately configured priority queue, then the logic programming engine actually implements Prim's algorithm for the low cost of an log(|V|) factor. But can this be directly expressed as a synthesis of weighted logic programming and linear logic programming? And can we do so while still maintaining a reasonable cost semantics? I don't know.

Traveling salesman problem

While minimum spanning tree is a greedy "existential" behavior of linear logic proof search, the weighted analogue of the Hamiltonian Path problem is just the Traveling Salesman problem - we not only want a Hamiltonian path, we want the best Hamiltonian path as measured by a straightforward extension of the notion of weight from weighted logic programming.

Not-linear logics?

Adding some linearity turned a single-source shortest path problem into a Hamiltonian path problem - when we turned vertices from persistent facts into linear resources, we essentially required each vertex to be "visited" exactly once. However, an affine logic interpretation of the same program would preserve the resource interpretation (vertices cannot be revisited) while removing the obligation - vertices can be visited once or they can be ignored altogether.

This makes the problem much more like the shortest path problem again. If edge weights are positive, then the shortest path never revisits a node, so it's for all intents and purposes exactly the shortest path problem again. If edge weights are negative, then disallowing re-visiting is arguably the only sensible way to specify the problem at all. Can this observation be generalized? Might it be possible to solve problems in (weighted) affine logic more easily than problems in weighted linear logic?

Principles of Constructive Provability Logic

So I think Bernardo and I have finally finished slaying the beast of a technical report we've been working on on-and-off all semester. I previously mentioned this tech report here. The intended audience for this paper is anyone who has read "A Judgmental Reconstruction of Modal Logic" (also known ubiquitously to CMUers as "Pfenning-Davies") and/or who has tasteful ideas about natural deduction and some notion of how modal logic works.

Unlike this blog post, which I wrote in 15 minutes while tired, Bernardo and I have worked very, very hard on trying making this report foundational and clear, and I'd definitely appreciate any feedback people have (large and small) since hopefully this won't be the last time I talk about constructive provability logic. Even if the feedback is that my jokes are really dumb and don't add anything to the paper (I should mention for Bernardo's sake that all the dumb jokes are my fault).

Principles of Constructive Provability Logic
Robert J. Simmons and Bernardo Toninho.
[PDF], [Agda tarball], and [Agda HTML]

Abstract: We present a novel formulation of the modal logic CPL, a constructive logic of provability that is closely connected to the Gödel-Löb logic of provability. Our logical formulation allows modal operators to talk about both provability and non-provability of propositions at reachable worlds. We are interested in the applications of CPL to logic programming; however, this report focuses on the presentation of a minimal fragment (in the sense of minimal logic) of CPL and on the formalization of minimal CPL and its metatheory in the Agda programming language. We present both a natural deduction system and a sequent calculus for minimal CPL and show that the presentations are equivalent.

The topic of the paper is "constructive provability logic" (CPL), a rich vein of logic that we've only just begun exploring.¹ The abstract and the introduction point out our primary reason for being interested in this logic: we want to give a general, satisfying, and proof-theoretic account for negation in logic programming. In fact, I've already gone out on a limb and written out the design of a distributed logic programming language based on a variant of CPL that I haven't quite-just-yet gotten around to entirely writing down. But I'm also just starting to implement the logic programming language, so it's not like I'm that far ahead of myself. The classical modal logic (which has about a dozen names but let's call it GL for Gödel-Löb) that we're intuitionisticing² about with has deep connections to everything from Gödel's incompleteness theorems to the denotational semantics of programming languages (it's the "modal" in the very modal models).

What's so special about this logic? Well, when you're working in the Kripke semantics of a modal logic, you should think of yourself as standing and a particular world and looking at some other worlds (these worlds are called accessible, and an accessibility relation determines which worlds are accessible). Maybe there aren't any! Maybe there are. Maybe you can see the world you're standing on, like being in a hall of mirrors. Maybe you can see one other world, and then beyond that world you can see back to the world you're standing on, like being in Pac-Man. The situation for GL and CPL is that not only can you not see yourself, you can't see forever - you can look past the accessible worlds to the worlds accessible from those (the "2-accessible" worlds, say) and then to the 3-accessible worlds... but this can't go on forever (jargon: the accessibility relation is "converse well-founded," there are no infinite ascending chains).

If you find yourself in a planetary system with a converse well-founded accessibility relation such as this one, the key is that, if you ever find your spaceship and go to one of those accessible worlds, there's now strictly less to see. Put another way, there's necessarily a little more going on where you're standing than in the places you're looking at. If this leads you to think that the places you can see are kind of an approximation of the place where you are, you're heading towards the approximation ("modal model"-esque) interpretation of GL. If you think "oh, the little more going on could refer to logical consistency," then you're heading towards the "provability" interpretation of GL. Perhaps the provability interpretation will inspire you to send a logician on every world and allow each logician to reason about the logical consistency of all the logicians he can see.³ Sure, you'll never get enough watchers for all the watchmen, but that is an occupational hazard of modern mathematics.

Anyway, I'll stop there: hopefully the details in the tech report are much, much clearer than the discussion in the preceding few paragraphs.

---

¹ I don't know when I started referring to my life as "working in the logic mines," it's really not fair to miners who have a really hard job that often isn't fun, unlike me. Maybe I'm just jealous of Mary's hat
² Intuitionisticing. v. To experimentally take a classical logic and try to deduce constructive, intuitionistic principles and proof theories out of it: Rowan and Alex were intuitionisticing about with propositional S4, and they both came up with things that seemed internally consistent but that were oddly incompatible.
³ Hey! It's a bad idea to use male pronouns to describe mathematicians! Okay, would you rather me be shooting female logicians into space for no compelling reason? Alright then.

Totally nameless representation

[Note: I am unaware of any truly original content in this post; when I say "we picked this up from Dan" it doesn't imply Dan worked it out himself; when I say "we worked this out" I don't have any reason to believe we were the first. Dan Licata in a comment lists some of the references to things we generally absorbed from him.]

This post is about two things. The first topic is a style of formalization in Agda that Bernardo Toninho and I picked up on from Dan Licata. The second topic is a way of establishing termination arguments that Bernardo and I worked out and used extensively in the Agda formalizaiton of several variants of Constructive Provability Logic, which I've mentioned before. Because I'm a bit perverse, I'll be using my own Agda Standard Library as the basis for this post; the code for this post can be found here - since it's a demo bound together with my library, technically I guess I'm supposed to keep the file at that link (though maybe not this post) in sync with the library as the library evolves.

Starting point: the simply-typed lambda calculus

This is a pretty standard Agda formalization of "Church-style" simply-typed lambda calculus terms. "Church-style," as opposed to "Curry-style," encodings only allow for the existence of well-typed terms.*

   open import Prelude

   infixr 5 _⊃_
   data Type : Set where
      con : String → Type
      _⊃_ : Type → Type → Type

   Ctx = List Type

   infixl 5 _·_
   data Term (Γ : Ctx) : Type → Set where
      var : ∀{A} → A ∈ Γ → Term Γ A
      _·_ : ∀{A B} → Term Γ (A ⊃ B) → Term Γ A → Term Γ B
      Λ : ∀{A B} → Term (A :: Γ) B → Term Γ (A ⊃ B)

The only non-obvious part of this encoding is that variables are represented by "dependent de Bruijn indices" - instead of a de Bruijn index being just a natural number, it's the pointer into its type in the context. The nice part about doing it this way is that you can define a very powerful notion of "generalized weakening" that is based on the "subset" partial order on contexts (Γ ⊆ Δ is a function mapping all the indices A ∈ Γ to indices A ∈ Δ).

   _⊆_ : Ctx → Ctx → Set
   _⊆_ = LIST.SET.Sub

   wk : ∀{Γ Δ A} → Γ ⊆ Δ → Term Γ A → Term Δ A 
   wk θ (var n) = var (θ n)
   wk θ (n1 · n2) = wk θ n1 · wk θ n2
   wk θ (Λ n) = Λ (wk (LIST.SET.sub-cons-congr θ) n)

The nice part about this definition, and one of the things I picked up on from Dan, is that we can then define the usual weakening, exchange, and contraction properties directly by using generalized weakening and the corresponding facts about the subset relation on lists (which are defined in my standard library).

   wken : ∀{Γ A C} → Term Γ C → Term (A :: Γ) C
   wken = wk LIST.SET.sub-wken

   exch : ∀{Γ A B C} → Term (A :: B :: Γ) C → Term (B :: A :: Γ) C
   exch = wk LIST.SET.sub-exch

   cntr : ∀{Γ A C} → Term (A :: A :: Γ) C → Term (A :: Γ) C 
   cntr = wk LIST.SET.sub-cntr

With that out of the way, we can talk about substitution, both the "obvious way" and the metric-indexed way Bernardo and I have used extensively.

Straightforward substitution

The obvious (for some value of obvious) and direct definition of substitution involves 1) generalizing the induction hypothesis to allow for even more additions (tm-subst) and 2) writing a variable substitution lemma that handles the case where the substituted-into term is a variable and we either perform the substitution, lower the de Bruijn index, or leaving the de Bruijn index alone (var-subst). The main theorem is inductive on the structure of the first term.

   subst : ∀{Γ A C} → Term Γ A → Term (A :: Γ) C → Term Γ C
   subst = tm-subst [] _
    where
      var-subst : ∀{A C} (Γ Γ' : Ctx)
         → Term Γ' A
         → C ∈ (Γ ++ [ A ] ++ Γ') 
         → Term (Γ ++ Γ') C
      var-subst [] Γ' n1 Z = n1
      var-subst [] Γ' n1 (S n) = var n
      var-subst (_ :: Γ) Γ' n1 Z = var Z
      var-subst (_ :: Γ) Γ' n1 (S n) = wken (var-subst Γ Γ' n1 n)
 
      tm-subst : ∀{A C} (Γ Γ' : Ctx) 
         → Term Γ' A
         → Term (Γ ++ [ A ] ++ Γ') C 
         → Term (Γ ++ Γ') C 
      tm-subst Γ Γ' n1 (var n) = var-subst Γ Γ' n1 n
      tm-subst Γ Γ' n1 (n · n') = tm-subst Γ Γ' n1 n · tm-subst Γ Γ' n1 n'
      tm-subst Γ Γ' n1 (Λ n) = Λ (tm-subst (_ :: Γ) Γ' n1 n)

To motivate the next step, I'll point out that the only reason we had to generalize the induction hypothesis is because of the lambda case - if we try to prove the theorem directly, we find ourselves in the position of having a Term Γ A and a Term (B :: A :: Γ) C; we can't apply the induction hypothesis directly on these two terms. We can apply wken to the first subterm and apply exch to the second subterm and call subst recursively, but now we can't establish termination on the structure of the second term, since we've passed it to the exch function, which changed its structure by replacing Zs with (S Z)s and vice versa.

Setting up a metric

The alternate solution I intend to present involves setting up a metric; this metric expresses the "shape" of a term, disregarding all binding. This is a three-step process: first we define a generic "tree" piece of data that can capture the shape of a term (disregarding binding), and second we define a copy of the Term datatype, called MTerm, that has a Metric as one of its indices.

   data Metric : Set where
      ○ : Metric
      _●_ : Metric → Metric → Metric
      > : Metric → Metric

   data MTerm (Γ : Ctx) : Type → Metric → Set where
      var : ∀{A} → A ∈ Γ → MTerm Γ A ○
      _·_ : ∀{A B m m'} → MTerm Γ (A ⊃ B) m → MTerm Γ A m' → MTerm Γ B (m ● m')
      Λ : ∀{A B m} → MTerm (A :: Γ) B m → MTerm Γ (A ⊃ B) (> m)

The third step is to show that we can freely get into and out of the metric; potentially we should also show that these two actions are an isomorphism, but I haven't run across the need to actually prove that. It really turns out that Agda does most of the work here...

   tm→ : ∀{Γ A m} → MTerm Γ A m → Term Γ A
   tm→ (var n) = var n
   tm→ (n1 · n2) = tm→ n1 · tm→ n2
   tm→ (Λ n) = Λ (tm→ n)

   →tm : ∀{Γ A} → Term Γ A → ∃ λ m → MTerm Γ A m
   →tm (var n) = , var n
   →tm (n1 · n2) = , snd (→tm n1) · snd (→tm n2)
   →tm (Λ n) = , Λ (snd (→tm n))

Now that we have our metric, we can prove a stronger and more useful version of the generalized weakening lemma: not only can we apply generalized weakening to terms, but the resulting term has the exact same shape (as shown by the fact that the same metric "m" appears as an index both to the function's argument and its conclusion.

   wkM : ∀{Γ Δ A m} → Γ ⊆ Δ → MTerm Γ A m → MTerm Δ A m
   wkM θ (var n) = var (θ n)
   wkM θ (n · n') = wkM θ n · wkM θ n'
   wkM θ (Λ n) = Λ (wkM (LIST.SET.sub-cons-congr θ) n)

We don't need to prove weakening twice; our previous weakening lemma is just a simple consequence of this new, stronger one:

   wk : ∀{Γ Δ A} → Γ ⊆ Δ → Term Γ A → Term Δ A 
   wk θ n = tm→ (wkM θ (snd (→tm n)))

Substitution with the metric

With the metric in tow, substitution is straightforward. Termination is established by induction on the metric of the second term. Note the use of both wken (weakening outside of the metric) and exchM (exchange inside the metric) in the lambda case.

   subst : ∀{Γ A C} → Term Γ A → Term (A :: Γ) C → Term Γ C
   subst n1 n2 = substM n1 (snd (→tm n2))
    where
      substM : ∀{Γ A C m} → Term Γ A → MTerm (A :: Γ) C m → Term Γ C
      substM n1 (var Z) = n1
      substM n1 (var (S n)) = var n
      substM n1 (n · n') = substM n1 n · substM n1 n'
      substM n1 (Λ n) = Λ (substM (wken n1) (exchM n))

In this example, it's not clear that we've saved much work: setting up the metric was a lot of boilerplate, though it is straightforward; the benefit that we gained in terms of proof simplicity was primarily an artifact of Agda's pattern matching: either a variable was the first variable in the context (and therefore represented by the de Bruijn index Z), or it was later in the context. So this example isn't the world's best argument for this style, but in the more complex logics that Bernardo and I dealt with, we found that this technique seemed, of all the approaches we could think of, to be the one least likely to fail on us.

Comments

Dan's said on a couple of occasions that he thinks there are less painful ways of doing this sort of thing, existing Agda techniques that avoid the annoying duplication of data types. My understanding is also that there is a not-totally-integrated notion of "sized types" in Agda that could maybe handle this sort of thing, but that the way it works is by defining metrics that are only natural numbers. It seems like a step backwards, somehow, if we go from structural induction to natural number induction. Furthermore, sized types based on natural numbers would almost certainly fail to handle the vaguely insane termination arguments that come up in constructive provability logic.

Totally nameless representations?

The germ of this post comes from a conversation with Chris Casinghino at UPenn back in May. He was working on extending this sort of simple representation in a way that was similarly-insane but mostly unrelated to constructive provability logic. Our problems were different; he placed the blame for some of the difficulties he encountered on the "sillyness of using all de bruijn indices instead of a locally nameless encoding," which was a response that I initially found puzzling. I've since decided that my puzzlement was the result of the fact that he was thinking of the specific thing he was doing in terms of programming languages, and I was thinking about the thing I was doing (constructive provability logic) in terms of logic - my guess is that we're both so used to working on both sides of the Curry-Howard correspondence that it wouldn't have occurred to us that this might make a difference!

From a programming languages perspective, we have programs and typing derivations that show programs to be well typed; the locally nameless encoding gives you the ability to apply the exchange or weakening lemma and get a new typing derivation that says that the same term is still well typed. That wasn't the case for our original "Church-style" lambda calculus terms. In my current view, that's because a "Church-style" lambda calculus term is more like the typing derivation than it is like a term. It's a typing derivation without the term it's typing; in other words, it's a proof in natural deduction form! And what Bernardo and I was using was something that, for our purposes, was just as good as a derivation that the same term was well typed in the exchanged context - we got that the same metric was associated with the exchanged proof term.

In other words, it seems that, for the purposes of termination arguments, the metric serves the same purpose a locally nameless proof term does. Certainly it avoids the "silliness of using all de Bruijn indices," as it uses none whatsoever, hence the mostly-joking title of this post. However, it's quite possible I'm off base; I'd be interested in what people more versed in locally nameless representation thought. I should add that I certainly think it is possible to do an intrinsically typed locally nameless representation; you'd just have to have (at minimum) the free variables be aware of their type. If you were interested primarily in representing a programming language that might even be the right thing to do; but the totally nameless metrics seem to be an easier fit for developments where the primary interest is in the logic side of the correspondence.

* Shameless plug for my advisor Frank Pfenning's excellent essay, "Church and Curry, Combining Intrinsic and Extrinsic Typing" which talks about properties of Church-style versus Curry-style encodings and relates them to subtyping and work by William Lovas.

P.S. This blog post has been about Agda; the first time I used this kind of tree structural metric on terms was in Twelf, when (on a challenge from John Boyland) I showed a bijection between HOAS and de Bruijn form representations of the terms of an untyped (or, if you prefer, "Curry-style") lambda calculus terms.

That curious termination argument

Quick, does the SML function norm terminate on all tree-valued inputs?

  datatype tree 
     = Nil 
     | Node of tree * int * tree

  fun norm Nil = Nil
    | norm (Node (Nil, x, t)) = 
         Node (Nil, x, norm t)
    | norm (Node (Node (t1, x, t2), y, t3)) = 
         norm (Node (t1, x, (Node (t2, y, t3))))

And if so, why?

This came from a post on the Theoretical Computer Science StackExchange asking about the theorem that, if two trees agree on their in-order traversals, then they are equivalent up to rotations. The "simple and intuitive" result mentioned in that post is a constructive proof which relies on the same termination ordering as the norm function. And it's also not terribly difficult to see why the function should terminate - it's a lexicographic termination argument: either the tree loses a node (the second case) or the tree keeps the same number of nodes and the depth of the left-most leaf decreases (the third case).

However, this sort of problem comes up not-terribly-infrequently in settings (like Agda) where termination must be established by structural induction, and the preceding argument is not structurally inductive on trees. Whenever I encounter this it always drives me crazy, so this is something of a note to myself.

Solution

The solution that works great for this sort of function in a dependently typed language is to define a judgment over terms that captures precisely the termination ordering that we will want to consider:

  data TM {A : Set} : Tree A -> Set where
    Done : TM Nil
    Recurse : {x : A}{t : Tree A}
       -> TM t
       -> TM (Node Nil x t)
    Rotate : {x y : A}{t1 t2 t3 : Tree A} 
       -> TM (Node t1 x (Node t2 y t3))
       -> TM (Node (Node t1 x t2) y t3)

Then (and this is really the tricky part) we have to write the proof that for every tree t there is a derivaiton of TM t. The key, and the reason that I always have to bend my brain whenever I encounter a termination argument like this one, is the append helper function.

  metric : {A : Set} (t : Tree A) -> TM t
  metric Nil = Done
  metric (Node t1 x t2) = helper t1 (metric t2)
    where
      append : {A : Set}{t1 t2 : Tree A} -> TM t1 -> TM t2 -> TM (t1 ++> t2)
      append Done t2 = t2
      append (Recurse t1) t2 = Recurse (append t1 t2)
      append (Rotate t1) t2 = Rotate (append t1 t2)

      helper : {A : Set} {x : A}{t2 : Tree A} 
         (t1 : Tree A) 
         -> TM t2
         -> TM (Node t1 x t2)
      helper Nil tt = Recurse tt
      helper (Node t1 x t2) tt = Rotate (helper t1 (append (helper t2 Done) tt))

Now it's trivial to write a version of the norm function that Agda will treat as terminating, because I just pass in an extra proof of TM t, and the proof proceeds by trivial structural induction on that proof.

  norm : {A : Set} -> Tree A -> Tree A
  norm t = helper t (metric t)
    where
      helper : {A : Set} -> (t : Tree A) -> TM t -> Tree A
      helper Nil Done = Nil 
      helper (Node Nil x t) (Recurse tm) =
         Node Nil x (helper t tm)
      helper (Node (Node t1 x t2) y t3) (Rotate tm) = 
         helper (Node t1 x (Node t2 y t3)) tm

The Agda code for the above is here. Are there other ways of expressing this termination argument in Agda that make as much or more sense? One approach I fiddled with was presenting a tree indexed by (1) the total number of nodes in it and (2) the depth of the left-most leaf:

  data ITree (A : Set) : NatT → NatT → Set where
    Nil : ITree A Z Z
    Node : ∀{total1 total2 left1 left2}
       -> ITree A left1 total1 
       -> A 
       -> ITree A left2 total2
       -> ITree A (1 +n left1) (1 +n (total1 +n total2))

However, due to the complexity of the dependent equality reasoning, I couldn't get Agda to believe the intuitive termination argument I presented at the beginning.

Trees have normal forms under rotation

Once the above argument works, it's not difficult to prove the theorem mentioned on TCS StackExchange; here's the Agda proof.

[Update Nov 15, 2010] Over at reddit, Conor McBride says "When someone asks "how do I show this non-structural function terminates?", I always wonder what structurally recursive function I'd write instead." and then proceeds to answer that question by giving the appropriate structurally inductive functions grind and rot. Nice! His proof also introduces me to a new Agda built-in, rewrite, whose existence I was previously unaware of. Oh Agda release announcements, when will I learn to read you?

Type Inference, In and Out of Context

Our reading group read the 2010 MSFP paper Type Inference In Context by Adam Gundry, Conor McBride, and James McKinna (ACM link). This was mostly because not all of us went to ICFP and not all of us that went to ICFP saw that MSFP talk (I was at HLPP and others were at WMM, IIRC man there are lots of acronyms in this sentence.)

Anyway, the people that went to the MSFP talk really liked the talk, so we read the paper. Some of it was confusing because state monad is not my native language. To understand it better, I re-implemented it in ML after the reading group. William and I then got into a discussion about how he had written a trying-to-be-very-clean implementation of the imperative type inference algorithm for MinML, so I adapted the algorithm further to the larger MinML language, and then adapted Williams code so that it ran in parallel with mine. And then I decided I wanted to throw the whole thing on my door as a parallel-corpus sort of thing.

The result is an impossibly sized PDF poster that I can turn into 6 tabloid sheets and put on my door, titled "Type Inference, In & Out of Context." It isn't aimed at being particularly introductory, but if you have read the MSFP paper it may be helpful as a guide to ML transfer, and I found the comparison to the imperative version of type inference quite enlightening.

There's a secondary interesting question here: what are good ways to present large pieces of literate code for dissemination? I kind of like this narrated poster form, especially for parallel corpuses, and I like literate Twelf things like the page on lax logic, but because I haven't had a lot of feedback and haven't been a reader of a lot of these sorts of things, I don't know how good I am at pulling it off. I'd appreciate feedback!

[Update Nov 18, 2010] Michael Sullivan notes that one aspect of "good ways to present large pieces of literate code" is actually providing the code so it doesn't have to be ineffectually cut and pasted from a pdf. The code is available in three files: typebase.sml (the language definition, snoc lists, and cons lists), typenoctx.sml (the imperative algorithm), and typeinctx.sml (the pure algorithm).

The variant record update problem

Now, for something completely different...

I've been helping out with the design and implementation of a languge called C₀ that is being used in a new course at Carnegie Mellon, 15-122 Principles of Imperative Computation. I'm giving my own point of view here, but I'd say that the goals of this language were four-fold:

• Programs should be memory safe (a pointer either contians NULL or the address of valid, allocated memory, and you can't read off the end of an array).
• The language should have no unspecified behavior. This is related to the point above ("oh, you did something undefined here so it's not my fault this pointer got decremented by 17 afterwards") but is still a distinct point - OCaml can be memory safe without specifying the order of evaluation of function arguments, for instance.
• Programs (at least the family of programs required to do homework tasks for 15-122) should look and act like C programs. (Featherweight Java programs act, but do not look, like Java programs.) And not "more or less" the same as C - GCC should basically be a viable way of compiling C₀ programs if they don't rely on behavior that is specified in C₀ but unspecified in C.
• The language should be amenable to garbage collection.

The language design process is primarily the work of Rob Arnold (who just presented his master's thesis yesterday) and his advisor, Frank Pfenning (also my advisor), who is teaching 15-122.

After Rob Arnold's defense, he, William Lovas, and I got into a discussion about adding unions in a safe way to the C₀ language. In the process we had to re-derive the fundamental problem with having remotely C-like unions in memory-safe programming languages. I am 90% certain that this is what the literature occasionally alludes to as "the variant record update problem." This is me writing that down so I won't have to derive it for myself yet again.

A piece of "reasonable" C, using unions

It is often the clearest if we think of all data in C as simply a bundle of bits; unions in C seem mostly like a way of providing different "views" for reading and writing into a bundle of bits. This is pretty well-illustrated by the following example, which we can then use to explain a very old problem with trying to tame this kind of union and treat it as a sum type or tagged unions in a memory-safe way.

  1.  typedef struct pair { 
  2.    unsigned char fst; 
  3.    char snd;
  4.  } pair;
  5.  typedef union {
  6.    unsigned short inj1;
  7.    pair inj2;
  8.  } foo;
  9.  int f(foo* foo) {
  10.   foo->inj1 = 1536;
  11.   return 7;
  12. }
  13. int main() {
  14.   foo foo;
  15.   foo.inj1 = 1535; 
  16.   // foo = Inj1(1535)
  17. 
  18.   foo.inj2.fst = 9;
  19.   foo.inj2.snd = 24; 
  20.   // foo = Inj2(9, 24)
  21. 
  22.   foo.inj2.fst = f(&foo); 
  23.   // WTF? Is foo Inj1 or Inj2?
  24. 
  25.   return 1;
  26. }

So, in C, we could pretty reasonably predict what should happen here given three pieces of information:

1. The size of a char and a short. (A char is 1 byte and a short is 2 bytes, in this case.)
2. The way C lays out structs in memory. (This is actually reasonably well-defined.)
3. The "endian-ness" of the machine we're working on. (I just worked it out from observerd results, myself: I can never remember which is which.)

In particular, this is what the 16 bits of stack storage allocated to foo looks like at various points in this program:

                       01234567 89ABCDEF
                       |  fst  |  snd  |
  At line 16 (in main) 11111111 10100000
  At line 20 (in main) 10010000 00011000
  At line 11 (in f)    00000000 01100000
  At line 23 (in main) 11100000 01100000

The assignment in f() happened before the crazy assignment was complete, writing a valid 16-bit short into the 2 bytes available to it. Then, the crazy assignment completed after f() returned, causing the first byte of that 2-byte short to get overwritten with the integer value 7 that was returned from f.

A non-starter

The basic idea that everyone has when trying to turn an unsafe language with untagged unions into a tagged language with tagged unions is "all we need to do is add tags and check them at the correct time." This example shows that there is a more fundamental problem, because there are a lot of different arguments for what the code above should even do in a safe programming language. The C semantics don't work: if foo.inj1 and foo.inj2.snd were pointers, then at line 23 foo can not safely be tagged as inj1 (part of its pointer got overwritten by the number 7) or as inj2 (because the second component is a pointer that got partially overwritten by a pointer in f().

We came up with four alternatives for what could mean, and none of us could agree on any one option; this is, of course, a sure sign that none of them make much sense.

1. Check, throw an error ("the safe option"). When we make an assignment into a union tagged with inj2, we're asserting that when the right-hand side finishes evaluating to a value, that tag will still be inj2. We have to check, after evaluating the right-hand-side to a value, that this property was maintained - and it's a runtime error if that isn't the case, kind of like running off the end of an array. Technically, this is a bit difficult, but it's certainly possible.
2. Re-initialize memory. C₀ has a notion of default values; whenever we allocate heap space for a new integer, that integer is 0. We'd actually want, after the assignment on line 18, to initialize the value of foo.inj2.snd to a default value (again, if it's a pointer we'd want to be sure it's NULL rather than some arbitrary string of bits that was there before). So, when we're ready to finally write a value, we check its tag - if the tag is wrong, we re-initialize it with the right tag and then perform the assignment; this is what happened on line 18. On line 22, it means that, because f() set the tag of foo to inj1 and we're making an assignment into inj2, we re-initialize the union as an inj2 and then perform the assignment. At line 23, foo has the tag inj2, foo.inj2.fst == 7, and foo.inj2.snd == 0.
3. Duplicate the entire union's memory block. Rather than after-the-fact tag checking, another option is to observe that we are reading into a union/struct, copy the entire union/struct into some temporary storage after evaluating the left-hand side, make the assignment into the temporarily storage, and then write the whole of the temporary storage back to its original location. In this case, at line 23 foo has the tag inj2, foo.inj2.fst == 7, and foo.inj2.snd == 24, the value it was set to before the assignment.
4. Secretly allocate memory. If we secretly say that a union is a pointer to some allocated memory, then when we change the tag we have to allocate some new memory. In this case, when f() changes the tag of foo, some new memory is allocated, tagged inj1, and the integer value 1536 is written there. foo is now a tag (inj1) and a pointer to the newly allocated memory, but the old memory (which foo pointed to before the assignment) is still in existence, and so we can safely write the value 7 to the memory location we came up with when we evaluated the left hand side of line 22. When we get to line 23, then, the memory where we just wrote the 7 has been orphaned, foo has a tag inj1, and contains the short integer value 1536. Note that this sort of trickery only makes any sense if we have a garbage-collected programming language; however, C₀ is a garbage collected language. However, it's also the only one of these four options that preserves the metaphor that a LHS evaluates to a memory location, a RHS evaluates to a value, and then the assignment stores the RHS value in the LHS memory location without further ado.

I'd be quite interested if anybody had information about real imperative programming languages that made any one of the four choices above, or some other choices.

What's actually going on here?

The real problem here is that C's notation for unions is deeply broken from a "mathematical perspective" if we want to think of unions as sum types. A sum type is not something you "project the inj1 field from" like a struct, it's something that you inject into the inj1^th branch of. So a much better notation than foo.inj1 = 4 is foo = inj1(4). We would think of this use of inj1 as somewhat equivalent to a constructor in ML, which leads us to a better understanding of the problem - when injecting into the inj2 branch, it's clear from the constructor notation that we need assign all the constituent values at the same time: foo = inj2(1,2). If this was the only way we could write to inj2, it would remove the difference between options 2 and 3 above - we would have to be clear in advance what we expected foo.inj2.snd to be, that's what it means to write into a branch.

Something like this solution is what was adopted in Ada, if we can believe the following caveat in the Ada Wikibook:

When "mutating" a record, you must assign all components of the variant structure which you are mutating at once, replacing the record with a complete variant structure.

This really seems like it would be the only remotely correct way of dealing with the problem.

Conclusion

Should unions be added to C₀, and how? Well, I don't actually have too much of a dog in that fight, and even if I did it's not my decision. Because we don't have "struct literal" values, we're unable to write something like foo.inj2 = { fst = 1, snd = 2 }, so the mostly-reasonable Ada solution is unavailable. A first step might be to disallow structs inside of unions, which means that every union can only ever contain one thing. This prevents the awkward question of "what is this other part of the union after the assignment" from ever arising as an issue - which is really the distinction between options 2 and 3 above.

The restriction of union members to "small values only" (the C₀ way of saying "no structs") is limiting from the perspective of C code that one might imagine wanting to write (and is therefore problematic for the goal that "good C₀ programs look like good C programs,") but it seems preferable to any of the four options above. In particular, if whenever you wanted to have a struct in a union you instead had a struct pointer, that would basically amount to implementing Option 4 in a non-secretive way.

Natural deduction and sequent calculus - united in a polarized linear framework

In the last post I talked a little bit about what it means to give atomic propositions in a logical framework polarity. The main point I wanted to get around to was that if we have a proposition in the signature of the form P1⁺ ⊃ P2⁺ ⊃ P3⁺, then all the information contained in that rule is captured by this synthetic inference rule:

  Γ, P1+, P2+, P3+ ⊢ Q
  -------------------
  Γ, P1+, P2+ ⊢ Q

On the other hand, if I have a proposition in the signature of the form P1^- ⊃ P2^- ⊃ P3^-, then all the information contained in that rule is captured by this synthetic inference rule:

  Γ ⊢ P1-
  Γ ⊢ P2-
  --------
  Γ ⊢ P3-

By further mixing-and-matching the polarities of atomic propositions, we can get a whole host of synthetic inference rules.

First, a clarification

Before I get started with this post, I want to point out that in the last post I said something imprecise: that the strongest possible form of adequacy is to say that the synthetic inference rules induced by your signature have an exact correspondence with the "on-paper" inference rules. I then gave an example, saying that

  ∨L : (hyp A → conc C)
       → (hyp B → conc C)
       → (hyp (A ∨ B) → conc C)

corresponds to this expected synthetic inference rule

  Γ, hyp (A ∨ B), hyp A ⊢ conc C
  Γ, hyp (A ∨ B), hyp B ⊢ conc C
  -------------------------------- ∨L
  Γ, hyp (A ∨ B) ⊢ conc C

only if (hyp A) has positive polarity. But this isn't quite the right story, because from the definition of ∨L we know nothing about the contents of Γ, and our notion of adequacy with respect to the sequent calculus requires that our judgments take the form Γ ⊢ conc C where Γ contains only atomic propositions hyp A for some propositions A. So, really, this strongest possible notion of adequacy needs one additional puzzle piece, a generalization of what the Twelfers would call regular worlds. We can assume the conclusion of the derived rule is in the image of some "on paper" judgment, but we also need to verify that the premises will always end up similarly in the image of some "on paper" judgment.

Now, with that out of the way...

Representing natural deduction in LLF

The post today starts off working with a subset of the Linear Logical Framework (LLF) designed (in large part) by Cervesato. We can reason about specifications in this framework using Jason Reed's HLF/Twelf implementation. Essentially, we will be using this framework the same way we used it last week: defining a signature and looking at the synthetic inference rules that arise from that signature.

It has recently become common to see presentations of the canonical forms of a simply-typed lambda calculus presented in spine form; doing so removes a major source of unplesentless in the proof of global soundness/hereditary substitution. You do have to pay the piper, though: it is more difficult to handle the proof of global completeness/η-expansion in a spine form calculus. However, a Twelf proof that Frank Pfenning worked out in February '09, which uses something like a third-order premise, can successfully handle the proof of global completeness for a spine-form presentation of canonical forms. One version of this Twelf proof, which can be found here, is presented as a bunch of Twelf code without much commentary, and the current story arose in part due to my attempts to provide some commentary and intuition for this Twelf proof of eta expansion and generalize it to substructural logics.

In the process, I ended up investigating another way of presenting logic that is somewhere between a natural deduction and spine form presentation. A bit of Twelf code describing this presentation can be found here, but the key point is that, when we need to verify an atomic proposition Q, we pick some hypothesis A from the context and show that, from a use of A we can prove that Q can be used. This is basically what happens in spine form, but here the "spiney" things associate the opposite of the way they do in spine form presentations. It looks something like this:

  end : use A A.
  atm : hyp A -> use A (a Q) -> verif (a Q).
  ⊃I  : (hyp A -> verif B) -> verif (A ⊃ B).
  ⊃E  : use A (B1 ⊃ B2) -> verif B1 -> use A B2.

One thing that we've known for a long time is that the atomic proposition (use A B) is an instance of a pattern - it can be thought of as a Twelf representation of the linear funtion use A -o use B, in which case the rule end above is just the identity function λx.x.

But, since we're putting ourself conceptually in the territory of LLF, not the territory of LF/Twelf, we can represent the thing that is morally a linear function as an actual linear function. The main trick is appropriately using unrestricted implication -> versus linear implication -o in such a way that it controls the branch of the subproof that the linear assumption use B winds up in. The resulting signature looks much like a standard natural deduction presentation with a very non-standard transition between uses and verifications (the usual rule is just use (a Q) -> verif (a Q)) and a sprinkling of lollipops where we'd normally see arrows.

  atm : hyp A -> (use A -o use (a Q)) -> verif (a Q).
  ⊃I  : (hyp A1 -> verif A2) -> verif (A1 ⊃ A2).
  ⊃E  : use (A1 ⊃ A2) -o verif A1 -> use A2.
  ∧I  : verif A1 -> verif A2 -> verif (A1 ∧ A2).
  ∧E1 : use (A1 ∧ A2) -o use A1.
  ∧E2 : use (A1 ∧ A2) -o use A2.

We are interested, for the purpose of this presentation, in hypothetical judgments of the form (Γ; · ⊢ hyp A), (Γ; · ⊢ verif A), and (Γ; use A ⊢ use B), where Γ contains unrestricted facts of the form hyp A. In light of this, we can show the synthetic inference rules that result from the above signature.

  ---------------------------- hyp
  Γ, hyp A; · ⊢ hyp A 

  ---------------------------- use
  Γ; use A ⊢ use A 

  Γ; · ⊢ hyp A
  Γ; use A ⊢ use (a Q)
  ---------------------------- atm
  Γ; · ⊢ verif (a Q)

  Γ, hyp A1; · ⊢ verif A2
  ---------------------------- ⊃I
  Γ; · ⊢ verif (A1 ⊃ A2)

  Γ; use B ⊢ use (A1 ⊃ A2)
  Γ; · ⊢ verif A1
  ---------------------------- ⊃E
  Γ; use B ⊢ use A2

  Γ; · ⊢ verif A1
  Γ; · ⊢ verif A2
  ---------------------------- ∧I
  Γ; · ⊢ verif (A1 ∧ A2)

  Γ; use B ⊢ use (A1 ∧ A2)
  ---------------------------- ∧E1
  Γ; use B ⊢ use A1

  Γ; use B ⊢ use (A1 ∧ A2)
  ---------------------------- ∧E2
  Γ; use B ⊢ use A2

There are basically no surprises - the complete HLF/Twelf specification, including global soundness and completeness proofs, is essentially just a repeat of the most closely related related Twelf specification where the elimination rules in the signature look somewhat less unusual.

Switching up the polarity

Now, let us imagine that we add atoms with positive polarity to LLF in a way analagous to their addition in the previous post. Obviously (hyp A) is naturally positive, so we can make that change, but that is not the interesting point. Consider the derived rules if we *also* make (use A) positive and restrict our attention to sequents of the form (Γ; · ⊢ verif A) and (Γ; use A ⊢ use (a Q)).

  ---------------------------- use
  Γ; use (a Q) ⊢ use (a Q)

  Γ, hyp A; use A ⊢ use (a Q)
  ---------------------------- atm
  Γ, hyp A; · ⊢ verif (a Q)

  Γ, hyp A1; · ⊢ verif A2
  ---------------------------- ⊃I
  Γ; · ⊢  verif (A1 ⊃ A2)

  Γ; use A₂ ⊢ use (a Q)
  Γ; · ⊢ verif A1
  ---------------------------- ⊃E
  Γ; use (A₁ ⊃ A₂) ⊢ use (a Q)

  Γ; · ⊢ verif A1
  Γ; · ⊢ verif A2
  ---------------------------- ∧I
  Γ; · ⊢ (verif A1 ∧ verif A2)

  Γ; use A1 ⊢ use (a Q)
  ---------------------------- ∧I1
  Γ; use (A1 ∧ A1) ⊢ use (a Q)

  Γ; use A2 ⊢ use (a Q)
  ---------------------------- ∧I2
  Γ; use (A1 ∧ A1) ⊢ use (a Q)

While our previous formalizaiton was an interesting sort-of modified version of natural deduction, the result when we change the polarity of the atomic proposition (use A) is precisely a focused sequent calculus.

A few related points

There are a lot of other neat explorations to consider in the near vicinity of this topic. Among them are:

• Generalizing to a polarized, weakly-focused logic. I did most of this once, but there were some issues with my original proof.
• What's the precise natural deduction system that the system with weak focusing + inversion on negative propositions corresponds to? Does it correspond exactly to the style of natural deduction used by Howe in "Proof Search in Lax Logic"?
• Generalizing to a fully-focused logic (how close can we get, for instance, to the natural deduction system of Brock-Nannestad and Schürmann ("Focused Natural Deduction," LPAR 2010)?
• Can this generalize to a focused linear sequent calculus, or do I only get to use linearity once per specification? Could the machinery of HLF be used to work around that?
• The global soundness and completeness results that I established in HLF have the least amount of slickness possible - I basically just repeat the proof that I gave for the Twelf formalization without linearity. How close can we get to the intuition that the eta expansion theorem says use A -> verif A for all A?

Focusing and synthetic rules

So, I was trying to explain to some people at a whiteboard something that I thought was more generally obvious than I guess it is. So, post! This post assumes you have seen lots of sequent caculi and have maybe have heard of focusing before, but I'll review the focusing basics first. And here's the main idea: focusing lets you treat propositions as rules. This is not an especially new idea if you are "A Twelf Person," but the details are still a bit pecular.

Let's start with a little baby logical framework. Here are the types:

  A ::= A → A | P⁺ | P⁻

Those P⁺ and P⁻ are the atomic propositions, and there can be as many of them as we want for there to be.

Focusing, real quick

There are three judgments that we need to be worried about. Γ ⊢ [ A ] is the right focus judgment, Γ[ A ] ⊢ Q is the left focus judgment, and Γ ⊢ A is the out-of-focus judgment.

Okay. So focusing (any sequent caclulus presentation of logic, really) encourages you to read rules from the bottom to the top, and that's how the informal descriptions will work. The first set of rules deal with right-focus, where you have to prove A right now. If you are focused on a positive atomic proposition, it has to be available right now as one of the things in the context. Otherwise (if you are focused on a negative atomic proposition or A → B), just try to prove it regular-style.

  P⁺ ∈ Γ
  -----------
  Γ ⊢ [ P⁺ ] 

  Γ ⊢ P⁻
  ----------
  Γ ⊢ [ P⁻ ]

  Γ ⊢ A → B
  -------------
  Γ ⊢ [ A → B ]

The second set of rules deal with left-focus. One pecular bit: we write left focus as Γ[ A ] ⊢ Q, and by Q we mean either a positive atomic proposition P⁺ or a negative atomic proposition P⁻. If we're in left focus on the positive atom, then we stop focusing and just add P⁺ to the set of antecedents Γ, but if we're in left focus on a negative atomic proposition P⁻, then we must to be trying to prove P⁻ on the right right now in order for the proof to succeed. Then, finally, if we're left focused on A → B, then we have to prove A in right focus and B in left focus.

  Γ, P⁺ ⊢ Q
  ------------
  Γ[ P⁺ ] ⊢ Q

  -------------
  Γ[ P⁻ ] ⊢ P⁻

  Γ ⊢ [ A ]
  Γ[ B ] ⊢ Q
  ---------------
  Γ[ A → B ] ⊢ Q

Finally, we need rules that deal with out-of-focus sequents. If we have an out-of-focus sequent and we're trying to prove P⁺, then we can go ahead and finish if P⁺ is already in the context. There is no rule for directly proving A⁻, but if we have a positive or negative atomic proposition that we're trying to prove, we can left-focus and work from there. And if we're trying to prove A → B, we can assume A and keep on trying to prove B.

  P⁺ ∈ Γ
  -------
  Γ ⊢ P⁺
  
  A ∈ Γ 
  A is not a positive atomic proposition
  Γ[ A ] ⊢ Q
  ---------------------------------------
  Γ ⊢ Q

  Γ, A ⊢ B
  -----------
  Γ ⊢ A → B

There are a lot of different similar presentations of focusing, most of which amount to the same thing, and most of which take some shortchuts. This one is no different, but the point is that this system is "good enough" that it lets us talk about the two big points.

The first big point about focusing is that it's complete - any sequent caclulus or natural deduction proof system for intuitionstic logic will prove exactly the same things as the focused sequent calculus. Of course, the "any other sequent calculus" you picked probably won't have a notion of positive and negative atomic propositions. That's the second big point: atomic propositions can be assigned as either positive or negative, but a given atomic proposition has to always be assigned the same positive-or-negativeness (that positive-or-negativeness is called polarity, btw). And on a similar note, you can change an atomic proposition's polarity if you change it everywhere. This may radically change the structure of a proof, but the same things will definitely be provable. Both of these things, incidentally, were noticed by Andreoli.

Synthetic inference rules

An idea that was also noticed by Andreoli but that was really developed by Kaustuv Chaudhuri is the idea that, when talking about a focused system, we should really think about proofs as being made up of synthetic inference rules, which are an artifact of focusing. The particular case of unfocused sequents where the conclusion is an atomic proposition, Γ ⊢ Q, is a special case that we can call neutral sequents. The only way we can prove a neutral sequent is to pull something out of the context and either finish (if the thing in the context is the positive atomic proposition we want to prove) or go into left focus. For instance, say that it is the case that P⁻ → Q⁻ → R⁻ ∈ Γ. Then the following derivation consists only of choices that we had to make if we left-focus on that proposition.

          ...
          Γ⊢Q⁻
  ...     ------ ---------
  Γ⊢P⁻    Γ⊢[Q⁻] Γ[R⁻]⊢R⁻
  ------  ----------------
  Γ⊢[P⁻]  Γ[Q⁻→R⁻]⊢R⁻
  ------------------       
  Γ[P⁻→Q⁻→R⁻]⊢R⁻     P⁻ → Q⁻ → R⁻ ∈ Γ
  ------------------------------------
  Γ⊢R⁻

This is a proof that has two leaves which are neutral sequents and a conclusion which is a neutral sequent, and where all the choices (including the choice of what the conclusion was) were totally forced by the rules of focusing. Therefore, we can cut out all the middle steps (which are totally determined anyway) and say that we have this synthetic inference rule:

  P⁻ → Q⁻ → R⁻ ∈ Γ
  Γ ⊢ Q⁻
  Γ ⊢ P⁻
  -----------------
  Γ ⊢ R⁻

This synthetic inference rule is more compact and somewhat clearer than the rule with all the intermediate focusing steps. As a side note, proof search with the inverse method is often much faster, too, if we think about these synthetic inference rules instead of the regular rules: that's part of the topic of Kaustuv Chaudhuri and Sean McLaughlin's Ph.D. theses. Chaudhri calls these things "derived rules" in his Ph.D. thesis, but I believe he is also the originator of the terms "synthetic connective" and "synthetic inference rule."

Let's do a few more examples. First, let's look at a synthetic inference rule for a proposition that has positive atomic propositions in its premises:

           Q⁺∈Γ
  ...     ------ ---------
  Γ⊢P⁻    Γ⊢[Q⁺] Γ[R⁻]⊢R⁻
  ------  ----------------
  Γ⊢[P⁻]  Γ[Q⁺→R⁻]⊢R⁻
  ------------------       
  Γ[P⁻→Q⁺→R⁻]⊢R⁻     P⁻ → Q⁺ → R⁻ ∈ Γ
  ------------------------------------
  Γ⊢R⁻

By convention, when one of the premises is of the form Q⁺ ∈ Γ, we go ahead and write the premise Q⁺ into the context everywhere, so the synthetic inference rule for this proposition is:

  P⁻ → Q⁺ → R⁻ ∈ Γ
  Γ, Q⁺ ⊢ P⁻
  -----------------
  Γ, Q⁺ ⊢ R⁻

If the conclusion ("head") of the proposition is a positive atom instead of a negative one, then we end up with an arbitrary conclusion.

  ...      ....
  Γ⊢P⁻    Γ,Q⁺⊢S
  ------  -------
  Γ⊢[P⁻]  Γ[Q⁺]⊢S
  ----------------
  Γ[P⁻→Q⁺]⊢S        P⁻ → Q⁺ ∈ Γ
  ---------------------------------------
  Γ⊢R

The synthetic inference rule looks like this, where S is required to be an atomic proposition, but it can be either positive or negative:

  P⁻ → Q⁺ ∈ Γ
  Γ ⊢ P⁻
  Γ, Q⁺ ⊢ S
  ----------
  Γ ⊢ S

If we have a higher-order premise (that is, an arrow nested to the left of an arrow - (P⁻ → Q⁺) → R⁻ is one such proposition), then we gain new assumptions in some of the branches of the proof. Note that the basic "shape" of this rule would not be affected if we gave P⁻ or Q⁺ the opposite polarity - synthetic inference rules are a little less sensitive to the polarity of atoms within higher-order premises.

   ...  
  Γ,P⁻⊢Q⁺
  -------
  Γ⊢P⁻→Q⁺   
  ---------  ---------
  Γ⊢[P⁻→Q⁺]  Γ[R⁻]⊢R⁻
  --------------------       
  Γ[(P⁻→Q⁻)→R⁻]⊢R⁻     (P⁻ → Q⁺) → R⁻ ∈ Γ
  ---------------------------------------
  Γ⊢R⁻

The synthetic inference rule, one more time, looks like this:

  (P⁻ → Q⁺) → R⁻ ∈ Γ
  Γ, P⁻ ⊢ Q⁺
  ----------
  Γ ⊢ R⁻

Application to logical frameworks

One annoyance in all of these derived rules is that each of them had a premise like (P⁻ → Q⁺) → R⁻ ∈ Γ. However, in a logical framework, we usually define a number of propositions in some "signature" Σ, and consider these propositions to be always true. Therefore, given any finite signature, we can "compile" that signature into a finite set of synthetic inference rules, add those to our logic, and throw away the signature - we don't need it anymore, as the synthetic inference rules contain precisely the logical information that was contained in the signature. Hence the motto, which admittedly may need some work: focusing lets you treat propositions as rules.

This is a strategy that hasn't been explored too much in logics where atomic propositions have mixed polarity - Jason Reed and Frank Pfenning's constructive resource semantics papers are the only real line of work that I'm familiar with, though Vivek's comment reminds me that I learned about the idea by way of Jason from Vivek and Dale Miller's paper "A framework for proof systems," section 2.3 in particular. (They in turn got it from something Girard wrote in French, I believe. Really gotta learn French one of these days.) The big idea here is that this is expressing the strongest possible form of adequacy - the synthetic inference rules that your signature gives rise to have an exact correspondance to the original, "on-paper" inference rules.

If this is our basic notion of adequacy, then I claim that everyone who has ever formalized the sequent calculus in Twelf has actually wanted positive atomic propositions. Quick, what's the synthetic connective corresponding to this pseudo-Twelf declaration of ∨L in the sequent calculus?

  ∨L : (hyp A → conc C)
       → (hyp B → conc C)
       → (hyp (A ∨ B) → conc C)

If you thought this:

  Γ, hyp (A ∨ B), hyp A ⊢ conc C
  Γ, hyp (A ∨ B), hyp B ⊢ conc C
  -------------------------------- ∨L
  Γ, hyp (A ∨ B) ⊢ conc C

then what you wrote down corresponds to what we like to write in "on-paper" presentations of the intuitionstic sequent calculus, but it is not the correct answer. Twelf has only negative atomic propositions, so the correct answer is this:

  Γ ⊢ hyp (A ∨ B)
  Γ, hyp A ⊢ conc C
  Γ, hyp B ⊢ conc C
  -------------------------------- ∨L
  Γ ⊢ conc C

This is still adequate in the sense that complete on-paper sequent calculus proofs are in one-to-one correspondence with the complete LF proofs: the reason that is true is that, when I am trying to prove Γ ⊢ hyp (A ∨ B), by a global invariant of the sequent calculus I can only succeed by left-focusing on some hyp (A ∨ B) ∈ Γ and then immediately succeeding. However, the partial proofs that focusing and synthetic connectives give rise to are not in one-to-one correspondence.

In order to get the rule that we desire, of course, we need to think of hyp A as a positive atomic proposition (and conc C as negative). If we do that, then the first proposed synthetic inference rule is dead-on correct.

Poll

Hey, I'm kind of new at logicblogging and don't really know who is following me. This was really background for a post I want to write in the future. Background-wise, how was this post?

[Update Nov 11, 2010] Vivek's comments reminded me of the forgotten source for the "three levels of adequacy," Vivek and Dale's "A framework for proof systems," which is probably a more canonical source than Kaustuv's thesis for using these ideas for representation. Also, the tech report mentioned in Vivek's comment replays the whole story in intuitionistic logic and is very close to the development in this blog post.

Background to constructive provability logic

So after some off-line discussions, while I continue to feel like the natural-deduction based judgmental methodology really maybe isn't the best way to do the work of experimentally developing logics (you really want the sequent calculus version for that - but that's another post), it's an excellent storytelling device. The idea is that it should help you explain a logic that is initially non-intuitive to an audience that you're trying not to scare off.

I'm not even certain how fully I believe that, since I tend to like using sequent calculus presentations for more-or-less everything that isn't a programming language. However, this tech report, by forcing me to work through a lot of things very carefully, has clarified my views on a lot of things - in particular, I think I have a "modern formulation" of the judgmental methodology that neatly generalizes to things like substructural logics without going out of its way, while simultaneously doing a good job of putting on paper all the tricks I learned from Dan about formalizing logics in Agda.

My wildest hope is that this story can motivate to Random J. PLPerson not only what Bernardo and I are doing specifically, but also give the intuition behind a number of things I've learned from Noam Zeilberger and Dan Licata about the philosophy behind both higher-order focusing and behind doing logic in Agda, and without actually requiring any background with focusing or knowledge of Agda to get there. I'd be happy to hear from you whether you think I've succeeded: any criticism would be greatly appreciated. (Draft Technical Report: Constructive Provability Logic)

Local soundness and completeness are PL-like properties

Currently, I'm trying to write up a tech report that clearly and fully present a peculiar modal logic that I discovered with the help of another graduate student last spring. In this tech report, I'm trying to closely follow what I think is correct to call the judgmental methodology , a philosophy for designing logics that was first outlined by Martin Lof in the 1983 Siena lectures and was refined by Pfenning and Davies in the 1999 paper "A Judgmental Reconstruction of Modal Logic."

Something that I think I knew but that I hadn't ever fully internalized is the degree to which the developments and checks recommended by the judgmental methodology are much closer to what you want when defining a programming language (where type safety - progress and preservation - are primary concerns) than what you want when defining a logic (where consistency, which is a sort of normalization property, is a big concern).

A really, really high level picture of the methodology followed by Pfenning and Davies is this:

• Define a substitution principle
• Show that everything that looks it should be a reducible expression (redex) is actually, you know, reducible (local soundness)
• Show that everything that has an interesting type can be η-expanded (local completeness)
• Check that the substitution principle which you claimed to be true and possibly used in the previous two steps actually holds

Now, as it turns out, proving the property of local completeness gets you most of the way there to the property called global completeness, but local soundness is woefully inadequate to get what you might call global soundness, the property that given a proof with redexes you can reduce redexes over and over until you get a proof with no redexes anymore. What I think local soundness ensures is that you'll always be able to keep reducing things that looks like redexes unless there aren't any more things that look like redexes. But this is just a progress property, that everything that "looks like a redex" actually is one. The combined local soundness proofs additionally can be seen as the cases of a variant form of the preservation theorem called subject reduction - this means that the local soundness proofs demonstrate both (a sort of) progress property and (a sort of) preservation property.

Is it really the case that the only "more interesting" part of type safety theorems is the fact that programming languages have values - places where, in practice, you want to stop with all of this reducing business - and the safety proof has to show that these uses of values are somehow consistent with the desired progress theorem? And has the "progress-ey" part of local soundness been considered elsewhere? Certainly the preservation-ey part is well-known enough to have its own name, "subject reduction." It seems like the kind of discussion that would be natural to find in the hybrid child of Proofs and Types and TAPL, but I don't believe such a book exists.

Anticipating the future

I believe that I have finally knocked out this progress lemma, which was (appropriately enough) holding back progress on my thesis proposal. I will have to see for sure tomorrow. The difficulty is not in proving the progress theorem itself; the problem is in making the progress theorem anticipates the future appropriately.

Anticipating the future is impossible in general, but it is also one way to explain a major point of my thesis proposal. What do I mean when I say I want to anticipate the future? Consider the following rules describing a little programming language with addition:

 -------
 n value

 (σ, e₁) ↦ (σ', e₁')
 -----------------------------
 (σ, e₁ + e₂) ↦ (σ', e₁' + e₂)

 e₁ value
 (σ, e₂) ↦ (σ', e₂')
 -----------------------------
 (σ, e₁ + e₂) ↦ (σ', e₁' + e₂)

 n₁ + n₂ ⇓ n₃
 -----------------------------
 (σ, n₁ + n₂) ↦ (σ, n₃)

Depending on your background, you may be thinking what the hell is that or perhaps why did he add the σ things everywhere. Or perhaps you saw where I was going immediately, and thought "oh, Rob intends to extend this specification with some sort of imperative, mutable state at some point in the future." Which is really the point: this specification has some ugliness to it (the currently-unnecessary σ annotations) so that it can anticipate the future addition of a feature, namely state. If I wanted to anticipate parallel evaluation, on the other hand, or maybe exception handling, I would have to make additional choices now.

But without knowing (or guessing) that I want to add mutable references, the σ annotations seem awfully unmotivated. If one tried to write an Structural Operational Semantics specification for a simple thing like the addition of numbers that anticipated the addition of features like state, parallel evaluation, and exception handling, there would be a lot of unmotivated stuff hanging around dirtying up the specification. So the question becomes: is it possible to anticipate these future additions without making it utterly painfully obvious that we're anticipating these future additions? Several groups of people, at least three or four by my count, have answered "yes!" to this question, and they've answered them in different ways. I will talk about them, and about the particular answer I am exploring, in a future post (if I anticipate the future correctly!)

In the meantime, I'm trying to also make sure that the proofs of basic safety properties (such as progress and preservation lemmas) can be written to anticipate the future inclusion of language features dealing with state, parallel evaluation, and exception handling. I am increasingly confident that this will work, but then again, I can't see the future ;-).